遠心力なんて存在しない！？誰でもわかる遠心力の秘密

こんにちは、ともです。

コーヒーカップ（今そんな乗らねーか）に乗ったら速く回せば回すほど外に持っていかれそうに感じますよね。たぶんそれを遠心力と呼ぶことも知っていると思います。

そう！遠心力！今回は遠心力についてです。

僕が高校3年生のとき、通っていた塾の物理の先生が、

「遠心力なんてものは存在しないんだよ～。」

とか言ってました。

誤解を恐れずに言うとそうなんです、遠心力なんてものは存在しないんです。

で、厳密にいうとある見方でみると遠心力なんてものは存在せず、別の見方をすると遠心力が出てくる、というわけです。なんだかわけわからないですね。早速見ていきましょうか。

遠心力が存在しないってどういうこと？

そもそも遠心力って回っているものに対して働きますよね？コーヒーカップやジェットコースターなど。あと、地球もですね。あ、ちなみに地球では赤道付近で一番遠心力が働くので体重でお悩みの方は熱帯地域に住まわれたらちょっぴり体重が軽くなるはず！

さて、では円運動（くるくる回っている運動）について考えてみましょうか。

一匹のニコちゃんがひもにつながっていて回っているとしましょう。

はい、そこ。数式出てきただけで拒絶反応しないー。この数式は補助です。数式なくても感覚的に理解できます。

まず、これはそとから見ているパターンです。上にある目があなただと思ってください。外から見てわかることはぐるぐるニコちゃんが回っていること、ニコちゃんが受けている力は中心に向かって引っ張られている力だということですね。

外から見ているあなたは「あ、こいつ円運動してるな。」ということがわかります。すると、このニコちゃんには自動的に F=ma という式が成り立ちます。（これを運動方程式という）これは F という力を体重 m のやつに加えたら a という加速度を持った、ということです。今まで静止していたボールを急に投げると速さをもって飛んでいくでしょ？それと一緒。

．．．で説明終わりなんです。円運動なのに遠心力出てきてないでしょ？ただニコちゃんが糸に引っ張られているという力しかない。だってそれしか見えないんだもん。

「いかさまだ！」という声もあるかもしれないので、じゃあ実際に遠心力が出てくる場合を見てみましょう。

遠心力が出てくる場合

状況はさっきと一緒。でも今回違うのは、あなたはニコちゃんです。ニコちゃんの気持ちになってみてください。

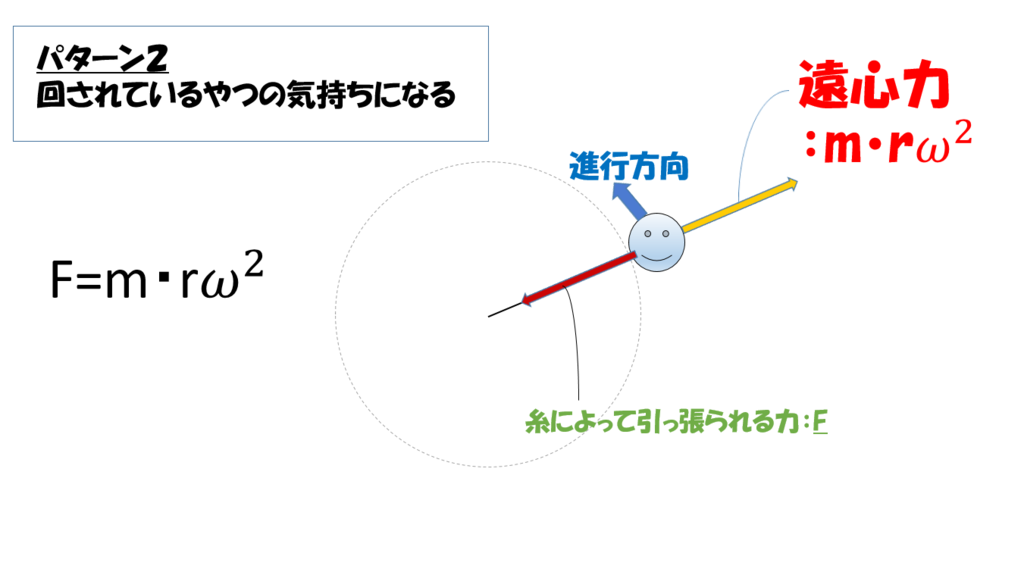
今から説明するから待って！拒絶しない！

あなたはニコちゃんでぐるぐる回されています。まずはさっきと一緒で糸に引っ張られてますよね？これがないとぐるぐる回れません。

ここでちょっと想像してみてください。もし、この状態で糸に引っ張られる力だけがあなた（ニコちゃん）にかかっていたらどうなりますか？

thinking time.....

...

....

.....

......

.......

........

.........

はい、終了ー。

答えはあなたが中心に向かって沈んで行っちゃう！でした。

だって、力それしか働いていないんでしょ、あなたには。じゃあ、そっちに引っ張られるよね。

それは困る。だってぐるぐる回っていたいから(笑)

じゃあ、ぐるぐる回っているためには反対向きにおんなじだけの力が必要（中心に沈まないため）。ということで反対向きに矢印が書いています。

これが遠心力！！（やっと言いたいことにたどり着いた）

理屈はこんな感じ。ニコちゃんをパシャって写真撮って、中心向きに引っ張られているのは当たり前だけどここで止まっておくためには反対向きに力必要だよね、というのが遠心力なんですね。

結論

2つの場合に分けて考えてきましたが、つまりは、

円運動している（ぐるぐる回っている）張本人だけがわかる力、それが遠心力

ということです。だって外から遠心力って見えないでしょ。想像はできるけど。

どっちでも同じ式になってることを確認してください。どっちにしろたどり着く結論は同じになります。

もしかしたら高校生が見てくれているかもしれないので言っておくと、遠心力は見かけの力です。なので、円運動の問題を解く際には多用しないほうがいいでしょう。円運動は確かに遠心力の公式をつかうとめちゃ早く解ける場合が多々ありますが、応用が利かなくなってきます。運動方程式で解く癖をつけましょう。

補足

「1つ目のパターンでも中心向きに引っ張られているじゃないか！沈まないのか！」という疑問が出てくるかもしれませんので少し補足を。

確かに中心向きの力（向心力）が加わっていますね。おっしゃる通りです。でも、これでいいんです。なぜなら、円運動とは加速度中心向きの運動だからです。

力の加わっている方向に加速度が発生します。なので、パターン1の場合中心向きに力が加わっているから加速度は中心向き。あ、加速度中心向きだじゃあ、これは円運動だね！とわかるわけです。少しあまのじゃく的ですが、円運動をするための条件は加速度が中心向きであるということです。

その加速度は円運動の場合 a=rω²、もしくは a=v²/r になります。（またいつか解説しようかな）

かなり身近な遠心力、実は外から見るか当事者になるかで違ってくるんですね。